線性搜尋（Linear Search）

又稱為 Sequential Search 循序搜尋，也就是從頭到尾一一比較個紀錄的鍵值，直到找到或找不到為止。

1. search 前，資料不需要經過排序
2. 可將資料存放在 Sequential Access(Linked List) 或 Random Access(Array) 的結構中

Time Complexity: O(n), n 為資料個數

我們用 Average Case 來看，位於第一個位置被找到需要比較 1 次，第二個位置需要 2 次，第 N 個位置需要 N 次，所以平均比較次數為：(1 + 2 + 3 + ... + N) / N = (N + 1) / 2 = O(N)

程式

int linear_search(int* arr, int n, int x)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == x)
            return i;
    return -1;
}

二分搜尋（Binary Search）

具有 Prune and Search（刪除搜尋法）或 Divided and Conquer 的搜尋法，而事先必須先將資料排序過，且必須保存資料於 Random Access 的環境。
步驟：

1. 先找出中間陣列中間之元素 M，並將欲搜尋之元素 X 與其比較。中間元素為頭尾 index 相加除以 2
2. 若 X == M，則找到
3. 若 X < M，則到 M 左邊之元素進行二分搜尋
4. 若 X > M，則到 M 右邊之元素進行二分搜尋

決策樹

例：有一個陣列[1~7]進行二分搜尋，畫出決策樹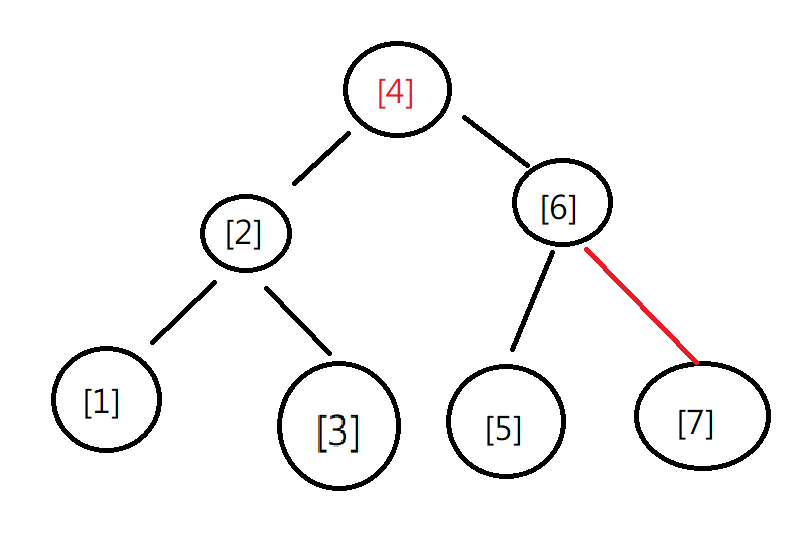

我們可以看到，出現在 level-i 的節點，比較次數為 i 次。
也可以看到，整棵樹最大比較次數 = 樹高。且決策樹又是高度最小化的 Binary Tree，Height = O(logn)

因此可以推斷 Binary Search 的 Time Complexity 為 O(logn)

遞迴時間函數

可以看到二分搜尋法每次遞迴，會進行一次比較，並將一個問題變成一個資料量一半的子問題

遞迴時間函數 T(n) = T(n/2) + 1, T(1) = 1

求解後即得出 T(n) = O(logn)

程式

int binarySearch_interation(int* arr, int l, int r, int x)
{
    while (l <= r) {
        int m = (l + r) / 2;
        if (arr[m] == x)
            return m;
        if (arr[m] < x)
            l = m + 1;
        else
            r = m - 1;
    }
    return -1; // not found
}

int binarySearch_recursion(int* arr, int l, int r, int x)
{
    if (l <= r) {
        int mid = (l + r) / 2;
        if (arr[mid] == x)
            return mid;
        else if (arr[mid] > x)
            return binarySearch_recursion(arr, l, mid - 1, x);
        else
            return binarySearch_recursion(arr, mid + 1, r, x);
    }
    return -1;
}